I have taught the following courses.
Math 260 (Introduction to Statistics) | 2025-2026 Spring
| Section | Times | Room |
| Section 1 | Wed 10:30–12:20 & Fri* 15:30–17:20 | A-Z27 |
| Section 2 | Mon 15:30–17:20 & Thu* 10:30–12:20 | SA-Z18 |
| Section 3 | Mon 10:30–12:20 &Wed* 15:30–17:20 | T-173 |
* Spare hour included in this session.
Textbook: Modern Mathematical Statistics with Applications, Jay L. Devore, Kenneth Berk, and Matthew A. Carlton, 3rd edition, Springer
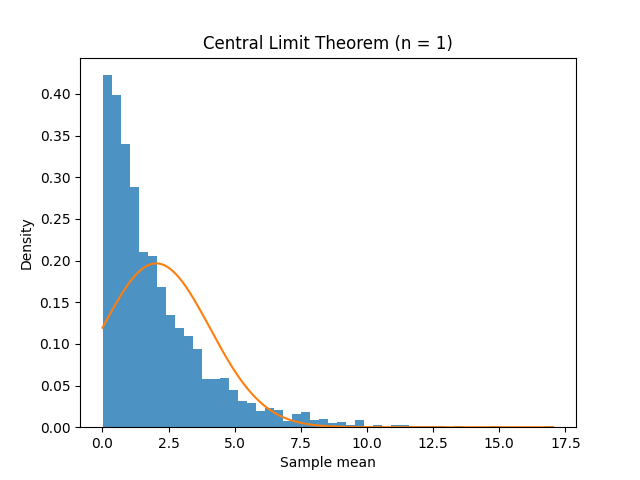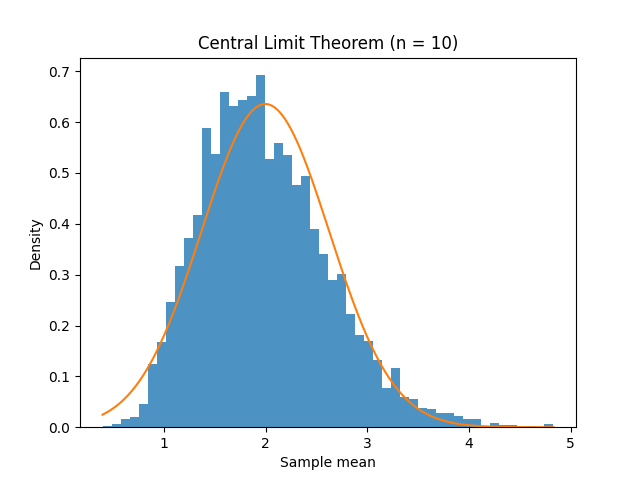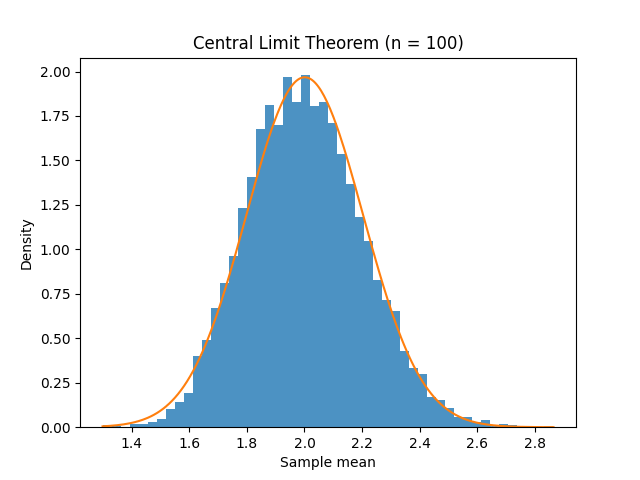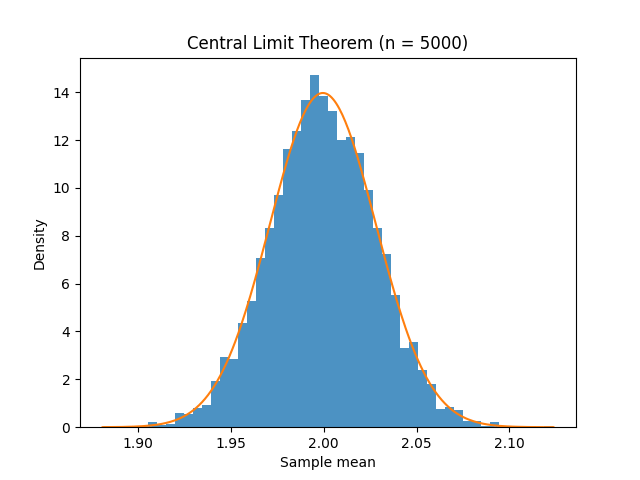
The simulation of the Central Limit Theorem.
Math 230 (Probability and Statistics for Engineers) | 2025-2026 Fall
| Section | Times | Room |
| Section 2 | Mon* 08:30–10:20 Wed 13:30–15:20 | T-173 |
| Section 3 | Mon* 15:30–17:20 Thu 10:30–12:20 | A-229 |
| Section 4 | Wed* 08:30–10:20 Fri 13:30–15:20 | T-272 |
| Office Hours | Fri 16:00-17:00 | SA-102 |
* Spare hour included in this session.
Textbook: Modern Mathematical Statistics with Applications, Jay L. Devore, Kenneth Berk, and Matthew A. Carlton, 3rd edition, Springer

Lecture Notes
Example Sheets
The course covers the following topics:
- Interpreting probabilities
- Axioms interpretations, and properties of probability
- Counting methods
- Conditional probability
- Independence
- Random variables
- Probability distributions for discrete random variables
- Expected value and standard deviation
- Moments and moment generating functions
- The binomial distribution
- Poisson distribution
- Other discrete distributions
- Probability density functions and cumulative distribution functions (Continuous random variables )
- Expected values and moment generating functions
- The normal (Gaussion) distribution
- Exponential and Gamma distributions
- Other continuous distributions
- Transformations of a random variable
- Jointly distributed random variables
- Expected values, covariance and correlation
- Linear combinations
- Statistics and their distributions
- Distribution of sample totals, means and proportions
- The Chi-squared, t and F distributions
- Concepts and criteria of point estimation
- Maximum likelihood estimation
- Confidence intervals
Math 106 (Introduction to Calculus II) | 2024-2025 Spring &Summer
Textbook: Calculus, Varberg – Purcell – Rigdon, 2007/9, Pearson New International Edition
The course covers the following topics:
- Antiderivatives
- Introduction to differential equations
- Introduction to area
- Definite integral
- The first fundamental theorem of calculus
- The second fundamental theorem of calculus
- Method of substitution
- Mean value theorem for integrals
- Area of a plane region
- Inverse functions and their derivatives
- Exponential and logarithmic functions
- Exponential growth and decay
- Inverse trigonometric functions
- Indeterminate forms and L’Hôpital’s Rule
- Compound interest
- Basic integration rules
- Integration by parts
- Trigonometric integrals
- Rationalizing substitutions
- Three-dimensional coordinate system
- Functions of several variables
- Partial fractions
- Partial derivatives
- The chain rule
- Maxima and minima
- The second partial derivative test
- The method of Lagrange multipliers
Below are some selected quizzes from the course.
Math 105 (Introduction to Calculus I) | 2024-2025 Fall
Textbook: Calculus, Varberg – Purcell – Rigdon, 2007/9, Pearson New International Edition
The course covers the following topics:
- Real numbers
- Inequalities and absolute value
- Lines and circles
- Graphs of equations
- Functions and their graphs
- Operations on functions
- Trigonometric functions
- Introduction to limits
- Limit theorems
- Limits involving trigonometric functions
- Limits at infinity
- Infinite limits
- Asymptotes
- Continuity of functions
- Tangent lines
- The derivative
- Rules for finding derivatives
- Derivatives of trigonometric functions
- The chain rule
- Higher-order derivatives
- Implicit differentiation
- Related rates
- Maxima and minima
- Monotonicity and concavity
- Local extrema and extrema on open Intervals
- The mean value theorem
- Graphing functions
- Optimization problems
- Economic applications
Below are some selected quizzes from the course.